surface_legacy

Legacy data structures for surfaces built from polygons.

All surfaces in sage-flatsurf are built from polygons whose sides are identified by similarities. This module provides deprecated data structures to describe such surfaces. Currently, there are two fundamental such data structures, namely Surface_list and \(Surface_dict\). The former labels the polygons that make up a surface by non-negative integers and the latter can use arbitrary labels.

In principle there is nothing wrong with this approach. However, the implementation is plagued by feature creep so we tried to clean things up in 2023 and reimplemented these in flatsurf.geometry.surface.

All the surfaces here inherit from Surface which describes the contract that surfaces used to satisfy. As an absolute minimum, they implement Surface.polygon() which maps polygon labels to actual polygons, and Surface.opposite_edge() which describes the gluing of polygons.

EXAMPLES:

We built a torus by gluing the opposite sides of a square:

sage: from flatsurf import Polygon
sage: from flatsurf.geometry.surface import Surface_list

sage: S = Surface_list(QQ)
doctest:warning
...
UserWarning: Surface_list has been deprecated and will be removed in a future version of sage-flatsurf; use MutableOrientedSimilaritySurface instead
sage: S.add_polygon(Polygon(vertices=[(0, 0), (1, 0), (1, 1), (0, 1)]))
0
sage: S.set_edge_pairing(0, 0, 0, 2)
sage: S.set_edge_pairing(0, 1, 0, 3)

sage: S.polygon(0)
Polygon(vertices=[(0, 0), (1, 0), (1, 1), (0, 1)])
sage: S.opposite_edge(0, 0)
(0, 2)

flatsurf.geometry.surface_legacy.ConeSurface(surface, *args, **kwargs)

Refine the category of surface.

This function is deprecated and should not be used anymore.

EXAMPLES:

sage: from flatsurf import Surface_list, polygons, ConeSurface
sage: S = Surface_list(QQ)
sage: S.add_polygon(polygons.square())
0
sage: S.set_edge_pairing(0, 0, 0, 2)
sage: S.set_edge_pairing(0, 1, 0, 3)
sage: S = ConeSurface(S)
doctest:warning
...
UserWarning: ConeSurface() has been deprecated and will be removed in a future version of sage-flatsurf; there is no distinction between an (underlying) Surface and the SimilaritySurface types anymore.
Calling set_immutable() on this surface should determine the category of this surface automatically so calling ConeSurface() should not be necessary in this case.
You can still explicitly refine the category of a surface with _refine_category_() but this is not recommended.
We will now refine the category of this surface to make sure that it is in the Category of connected without boundary oriented cone surfaces.
sage: S.category()
Category of connected without boundary finite type oriented cone surfaces
sage: S.set_immutable()
sage: S.category()
Category of connected without boundary finite type translation surfaces

flatsurf.geometry.surface_legacy.DilationSurface(surface, *args, **kwargs)

Refine the category of surface.

This function is deprecated and should not be used anymore.

EXAMPLES:

sage: from flatsurf import Surface_list, polygons, DilationSurface
sage: S = Surface_list(QQ)
sage: S.add_polygon(polygons.square())
0
sage: S.set_edge_pairing(0, 0, 0, 2)
sage: S.set_edge_pairing(0, 1, 0, 3)
sage: S = DilationSurface(S)
doctest:warning
...
UserWarning: DilationSurface() has been deprecated and will be removed in a future version of sage-flatsurf; there is no distinction between an (underlying) Surface and the SimilaritySurface types anymore.
Calling set_immutable() on this surface should determine the category of this surface automatically so calling DilationSurface() should not be necessary in this case.
You can still explicitly refine the category of a surface with _refine_category_() but this is not recommended.
We will now refine the category of this surface to make sure that it is in the Category of connected without boundary oriented positive dilation surfaces.
sage: S.category()
Category of connected without boundary finite type oriented positive dilation surfaces
sage: S.set_immutable()
sage: S.category()
Category of connected without boundary finite type translation surfaces

class flatsurf.geometry.surface_legacy.ExtraLabel(value=None)

Used to spit out new labels.

flatsurf.geometry.surface_legacy.HalfDilationSurface(surface, *args, **kwargs)

Refine the category of surface.

This function is deprecated and should not be used anymore.

EXAMPLES:

sage: from flatsurf import Surface_list, polygons, HalfDilationSurface
sage: S = Surface_list(QQ)
sage: S.add_polygon(polygons.square())
0
sage: S.set_edge_pairing(0, 0, 0, 2)
sage: S.set_edge_pairing(0, 1, 0, 3)
sage: S = HalfDilationSurface(S)
doctest:warning
...
UserWarning: HalfDilationSurface() has been deprecated and will be removed in a future version of sage-flatsurf; there is no distinction between an (underlying) Surface and the SimilaritySurface types anymore.
Calling set_immutable() on this surface should determine the category of this surface automatically so calling HalfDilationSurface() should not be necessary in this case.
You can still explicitly refine the category of a surface with _refine_category_() but this is not recommended.
We will now refine the category of this surface to make sure that it is in the Category of connected without boundary oriented dilation surfaces.
sage: S.category()
Category of connected without boundary finite type oriented dilation surfaces
sage: S.set_immutable()
sage: S.category()
Category of connected without boundary finite type translation surfaces

flatsurf.geometry.surface_legacy.HalfTranslationSurface(surface, *args, **kwargs)

Refine the category of surface.

This function is deprecated and should not be used anymore.

EXAMPLES:

sage: from flatsurf import Surface_list, polygons, HalfTranslationSurface
sage: S = Surface_list(QQ)
sage: S.add_polygon(polygons.square())
0
sage: S.set_edge_pairing(0, 0, 0, 2)
sage: S.set_edge_pairing(0, 1, 0, 3)
sage: S = HalfTranslationSurface(S)
doctest:warning
...
UserWarning: HalfTranslationSurface() has been deprecated and will be removed in a future version of sage-flatsurf; there is no distinction between an (underlying) Surface and the SimilaritySurface types anymore.
Calling set_immutable() on this surface should determine the category of this surface automatically so calling HalfTranslationSurface() should not be necessary in this case.
You can still explicitly refine the category of a surface with _refine_category_() but this is not recommended.
We will now refine the category of this surface to make sure that it is in the Category of connected without boundary oriented half translation surfaces.
sage: S.category()
Category of connected without boundary finite type oriented half translation surfaces
sage: S.set_immutable()
sage: S.category()
Category of connected without boundary finite type translation surfaces

class flatsurf.geometry.surface_legacy.LabelWalker(surface, deprecation_warning=True)

Take a canonical walk around the surface and find the labels of polygons.

We start at the base_label(). Then the labels are visited in order involving the combinatorial distance from the base_label(), where combinatorial distance measures the minimal number of edges which need to be crossed to reach the polygon with a givel label. Ties are broken using lexicographical order on the numbers associated to edges crossed (labels are not used in this lexicographical ordering).

class LabelWalkerIterator(label_walker)

next()

edge_back(label, limit=None)

Return the “canonical” edge to walk through to get closer to the base_label, or None if label already is the base_label.

Remark: This could be slow on infinite surfaces!

edge_iterator(gluings=False)

find_a_new_label()

Finds a new label, stores it, and returns it. Returns None if we have already found all labels.

find_all_labels()

find_new_labels(n)

Look for n new labels. Return the list of labels found.

label_dictionary()

Return a dictionary mapping labels to integers which gives a canonical order on labels.

label_polygon_iterator()

label_to_number(label, search=False, limit=100)

Return the number associated to the provided label.

Returns an error if the label has not already been found by the walker unless search=True in which case we look for the label. We look by continuing to look for the label by walking over the surface visiting the next limit many polygons.

number_to_label(n)

Return the n-th label where n is less than the length.

polygon_iterator()

surface()

class flatsurf.geometry.surface_legacy.LabelsView(surface)

flatsurf.geometry.surface_legacy.RationalConeSurface(surface, *args, **kwargs)

Refine the category of surface.

This function is deprecated and should not be used anymore.

EXAMPLES:

sage: from flatsurf import Surface_list, polygons, RationalConeSurface
sage: S = Surface_list(QQ)
sage: S.add_polygon(polygons.square())
0
sage: S.set_edge_pairing(0, 0, 0, 2)
sage: S.set_edge_pairing(0, 1, 0, 3)
sage: S = RationalConeSurface(S)
doctest:warning
...
UserWarning: RationalConeSurface() has been deprecated and will be removed in a future version of sage-flatsurf; there is no distinction between an (underlying) Surface and the SimilaritySurface types anymore.
Calling set_immutable() on this surface should determine the category of this surface automatically so calling RationalConeSurface() should not be necessary in this case.
You can still explicitly refine the category of a surface with _refine_category_() but this is not recommended.
We will now refine the category of this surface to make sure that it is in the Category of connected without boundary oriented rational cone surfaces.
sage: S.category()
Category of connected without boundary finite type oriented rational cone surfaces
sage: S.set_immutable()
sage: S.category()
Category of connected without boundary finite type translation surfaces

flatsurf.geometry.surface_legacy.SimilaritySurface(surface, *args, **kwargs)

Refine the category of surface.

This function is deprecated and should not be used anymore.

EXAMPLES:

sage: from flatsurf import Surface_list, polygons, SimilaritySurface
sage: S = Surface_list(QQ)
doctest:warning
...
UserWarning: Surface_list has been deprecated and will be removed in a future version of sage-flatsurf; use MutableOrientedSimilaritySurface instead
sage: S.add_polygon(polygons.square())
0
sage: S.set_edge_pairing(0, 0, 0, 2)
sage: S.set_edge_pairing(0, 1, 0, 3)
sage: S = SimilaritySurface(S)
doctest:warning
...
UserWarning: SimilaritySurface() has been deprecated and will be removed in a future version of sage-flatsurf; there is no distinction between an (underlying) Surface and the SimilaritySurface types anymore.
Calling set_immutable() on this surface should determine the category of this surface automatically so calling SimilaritySurface() should not be necessary in this case.
You can still explicitly refine the category of a surface with _refine_category_() but this is not recommended.
We will now refine the category of this surface to make sure that it is in the Category of connected without boundary oriented similarity surfaces.
sage: S.category()
Category of connected without boundary finite type oriented similarity surfaces
sage: S.set_immutable()
sage: S.category()
Category of connected without boundary finite type translation surfaces

class flatsurf.geometry.surface_legacy.Surface(base_ring, base_label, finite, mutable, category=None, deprecation_warning=True)

Abstract base class of all surfaces that are built from a set of polygons with edges identified. The identifications are compositions of homothety, rotations and translations, i.e., similarities that ensure that the surface is oriented.

Concrete implementations of a surface must implement at least polygon() and opposite_edge().

To be able to modify a surface, subclasses should also implement _change_polygon, _set_edge_pairing, _add_polygon, _remove_polygon.

For concrete implementations of a Surface, see, e.g., Surface_list and Surface_dict.

INPUT:

• base_ring – the ring containing the coordinates of the vertices of the polygons

• base_label – the label of a chosen special polygon in the surface, see base_label()

• finite – whether this is a finite surface, see is_finite_type()

• mutable – whether this is a mutable surface; can be changed later with set_immutable()

EXAMPLES:

sage: from flatsurf.geometry.surface import Surface, Surface_list, Surface_dict

sage: S = Surface_list(QQ)
sage: isinstance(S, Surface)
True

sage: S = Surface_dict(QQ)
doctest:warning
...
UserWarning: Surface_dict has been deprecated and will be removed in a future version of sage-flatsurf; use MutableOrientedSimilaritySurface instead
sage: isinstance(S, Surface)
True

add_polygon(new_polygon, gluing_list=None, label=None)

Adds a the provided polygon to the surface. Utilizes gluing_list for the gluing data for edges (which must be a list of pairs representing edges of length equal to number of edges of the polygon).

If the parameter label is provided, the Surface attempts to use this as the label for the new_polygon. However, this may fail depending on the implementation.

Returns the label assigned to the new_polygon (which may differ from the label provided).

add_polygons(polygons)

change_base_label(new_base_label)

Change the base_label to the provided label.

change_edge_gluing(label1, edge1, label2, edge2)

Update the gluing so that (label1, edge1) is glued to (label2, edge2).

change_polygon(label, new_polygon, gluing_list=None)

Assuming label is currently in the list of labels, change the poygon assigned to the provided label to new_polygon, and glue the edges according to gluing_list (which must be a list of pairs of length equal to number of edges of the polygon).

change_polygon_gluings(label, glue_list)

Updates the list of glued polygons according to the provided list, which is a list of pairs (pp,ee) whose position in the list describes the edge of the polygon with the provided label.

This method updates both the edges of the polygon with label “label” and updates the edges listed in the glue_list.

graphical_surface(*args, **kwds)

Return a GraphicalSurface representing this surface.

By default this returns a cached version of the GraphicalSurface. If cached=False is provided as a keyword option then a new GraphicalSurface is returned.

All other parameters are passed on to GraphicalSurface or its process_options(). Note that this mutates the cached graphical surface for future calls.

EXAMPLES:

Test the difference between the cached graphical_surface and the uncached version:

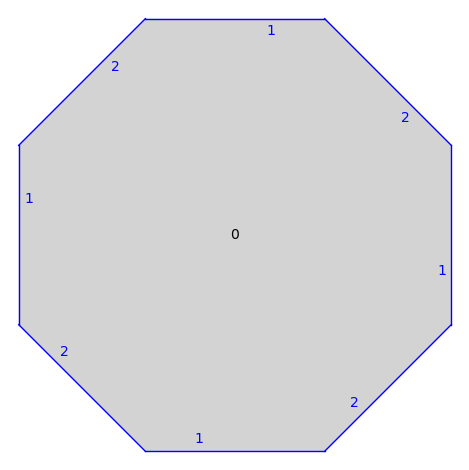
sage: from flatsurf import translation_surfaces
sage: s = translation_surfaces.octagon_and_squares()
sage: s.plot()
...Graphics object consisting of 32 graphics primitives

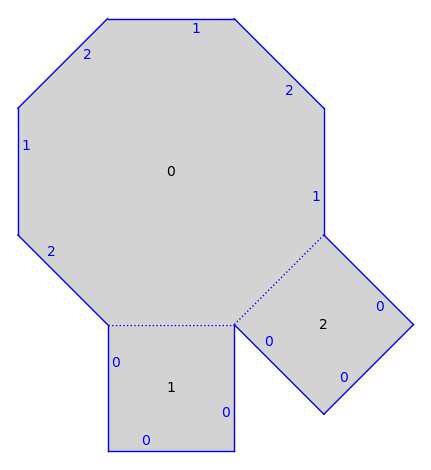
sage: s.graphical_surface(adjacencies=[]).plot()
...Graphics object consisting of 18 graphics primitives

is_finite_type()

Return whether or not the surface is finite.

is_mutable()

Return if this surface is mutable.

is_triangulated(limit=None)

EXAMPLES:

sage: import flatsurf
sage: G = SymmetricGroup(4)
sage: S = flatsurf.translation_surfaces.origami(G('(1,2,3,4)'), G('(1,4,2,3)'))
sage: S.is_triangulated()
False
sage: S.triangulate().codomain().is_triangulated()
True

label_iterator(polygons=False)

Iterator over all polygon labels.

Subclasses should consider overriding this method for increased performance.

labels()

num_polygons()

Return the number of polygons making up the surface, or sage.rings.infinity.Infinity if the surface is infinite.

This is a generic method. On a finite surface it will be linear time in the edges the first time it is run, then constant time (assuming no mutation occurs).

Subclasses should consider overriding this method for increased performance.

opposite_edge(label, e=None)

Given the label label of a polygon and an edge e in that polygon returns the pair (ll, ee) to which this edge is glued.

This method must be overridden in subclasses.

plot(*args, **kwds)

Return a plot of the surface.

The parameters are passed on to graphical_surface() and flatsurf.graphical.surface.GraphicalSurface.plot(). Consult their documentation for details.

EXAMPLES:

sage: import flatsurf
sage: S = flatsurf.translation_surfaces.veech_double_n_gon(5)
sage: S.plot()
...Graphics object consisting of 21 graphics primitives

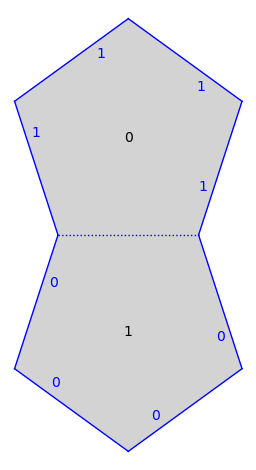
Keywords are passed on to the underlying plotting routines, see flatsurf.graphical.surface.GraphicalSurface.plot() for details:

sage: S.plot(fill=None)
...Graphics object consisting of 21 graphics primitives

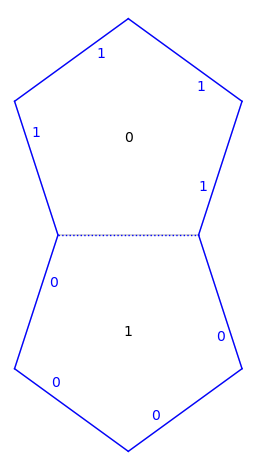
Note that some keywords mutate the underlying cached graphical surface, see graphical_surface():

sage: S.plot(edge_labels='gluings and number')
...Graphics object consisting of 23 graphics primitives

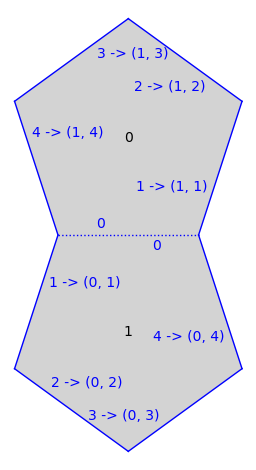
point(label, position, limit=None, ring=None)

Return the flatsurf.geometry.surface_objects.SurfacePoint of this surface at position in the polygon label.

INPUT:

• label – a label of a polygon in this surface, see label_iterator()

• position – a vector with coordinates in this surface’s base ring

EXAMPLES:

sage: from flatsurf import Polygon
sage: from flatsurf.geometry.surface import Surface_list

sage: S = Surface_list(QQ)
sage: S.add_polygon(Polygon(vertices=[(0, 0), (1, 0), (1, 1), (0, 1)]))
0
sage: S.set_edge_pairing(0, 0, 0, 2)
sage: S.set_edge_pairing(0, 1, 0, 3)

sage: S.point(0, (0, 0))
Vertex 0 of polygon 0

polygon(label)

Return the polygon with the provided label.

This method must be overridden in subclasses.

remove_polygon(label)

Remove the polygon with the provided label. Causes a ValueError if the base_label is removed.

roots()

set_default_graphical_surface(graphical_surface)

Replace the default graphical surface with the provided GraphicalSurface.

set_edge_pairing(label1, edge1, label2, edge2)

Update the gluing so that (label1, edge1) is glued to (label2, edge2).

set_immutable()

Mark this surface as immutable.

walker()

Return a LabelWalker which walks over the surface in a canonical way.

flatsurf.geometry.surface_legacy.SurfaceClass(surface, name, category, *args, **kwargs)

class flatsurf.geometry.surface_legacy.Surface_dict(base_ring=None, surface=None, copy=None, mutable=None, category=None, deprecation_warning=True)

A mutable Surface using a dict to store polygons and gluings.

Unlike Surface_list, this surface is not limited to integer labels. However, Surface_list is likely more efficient for most applications.

ALGORITHM:

Internally, we maintain a dict _p for storing polygons together with gluing data.

Each _p[label] is typically a pair (polygon, gluing_dict) where gluing_dict is maps other_label to other_edge such that opposite_edge(label, edge) returns _p[label][1][edge].

INPUT:

• base_ring – ring or None (default: None); the ring containing the coordinates of the vertices of the polygons. If None, the base ring will be the one of surface.

• surface – a surface or None (default: None); a surface to be copied or referenced (see copy). If None, the surface is initially empty.

• copy – boolean or None (default: None); whether the data underlying surface is copied into this surface or just a reference to that surface is kept. If None, a sensible default is chosen, namely surface.is_mutable().

• mutable – boolean or None (default: None); whether this surface is mutable. When None, the surface will be mutable iff surface is None.

EXAMPLES:

sage: from flatsurf import polygons, Surface_dict
sage: p=polygons.regular_ngon(10)
sage: s=Surface_dict(base_ring=p.base_ring())
doctest:warning
...
UserWarning: Surface_dict has been deprecated and will be removed in a future version of sage-flatsurf; use MutableOrientedSimilaritySurface instead
sage: s.add_polygon(p,label="A")
'A'
sage: s.change_polygon_gluings("A",[("A",(e+5)%10) for e in range(10)])
sage: s.change_base_label("A")
sage: s.set_immutable()
sage: TestSuite(s).run()

is_compact()

label_iterator(polygons=False)

Iterator over all polygon labels.

num_polygons()

Return the number of polygons making up the surface in constant time.

opposite_edge(p, e=None)

Given the label p of a polygon and an edge e in that polygon returns the pair (pp, ee) to which this edge is glued.

polygon(lab)

Return the polygon with label lab.

class flatsurf.geometry.surface_legacy.Surface_list(base_ring=None, surface=None, copy=None, mutable=None, category=None, deprecation_warning=True)

A fast mutable Surface using a list to store polygons and gluings.

ALGORITHM:

Internally, we maintain a list _p for storing polygons together with gluing data.

Each _p[label] is typically a pair (polygon, gluing_list) where gluing_list is a list of pairs (other_label, other_edge) such that opposite_edge(label, edge) returns _p[label][1][edge].

INPUT:

• base_ring – ring or None (default: None); the ring containing the coordinates of the vertices of the polygons. If None, the base ring will be the one of surface.

• surface – a surface or None (default: None); a surface to be copied or referenced (see copy). If None, the surface is initially empty.

• copy – boolean or None (default: None); whether the data underlying surface is copied into this surface or just a reference to that surface is kept. If None, a sensible default is chosen, namely surface.is_mutable().

• mutable – boolean or None (default: None); whether this surface is mutable. When None, the surface will be mutable iff surface is None.

EXAMPLES:

sage: from flatsurf import polygons, Surface_list, Polygon, similarity_surfaces
sage: p=polygons.regular_ngon(5)
sage: s=Surface_list(base_ring=p.base_ring())
doctest:warning
...
UserWarning: Surface_list has been deprecated and will be removed in a future version of sage-flatsurf; use MutableOrientedSimilaritySurface instead
sage: s.add_polygon(p) # gets label 0
0
sage: s.add_polygon( (-matrix.identity(2))*p ) # gets label 1
1
sage: s.change_polygon_gluings(0,[(1,e) for e in range(5)])
sage: # base label defaults to zero.
sage: s.set_immutable()
sage: TestSuite(s).run()

We surgically add a square into an infinite billiard surface:

sage: p = Polygon(vertices=[(0,0),(4,0),(0,3)])
sage: s = similarity_surfaces.billiard(p)
sage: ts=s.minimal_cover(cover_type="translation").copy(relabel=True, mutable=True)
doctest:warning
...
UserWarning: copy() has been deprecated and will be removed from a future version of sage-flatsurf; for surfaces of finite type use MutableOrientedSimilaritySurface.from_surface() instead.
Use relabel({old: new for (new, old) in enumerate(surface.labels())}) for integer labels. However, there is no immediate replacement for lazy copying of infinite surfaces.
Have a look at the implementation of flatsurf.geometry.delaunay.LazyMutableSurface and adapt it to your needs.
sage: # Explore the surface a bit
sage: ts.polygon(0)
Polygon(vertices=[(0, 0), (4, 0), (0, 3)])
sage: ts.opposite_edge(0,0)
(1, 2)
sage: ts.polygon(1)
Polygon(vertices=[(0, 0), (0, -3), (4, 0)])
sage: s = ts
sage: l=s.add_polygon(polygons.square(side=4))
sage: s.change_edge_gluing(0,0,l,2)
sage: s.change_edge_gluing(1,2,l,0)
sage: s.change_edge_gluing(l,1,l,3)
sage: print("Glued in label is "+str(l))
Glued in label is 2
sage: count = 0
sage: for x in ts.gluings():
....:     print(x)
....:     count=count+1
....:     if count>15:
....:         break
((0, 0), (2, 2))
((0, 1), (3, 1))
((0, 2), (4, 0))
((2, 0), (1, 2))
((2, 1), (2, 3))
((2, 2), (0, 0))
((2, 3), (2, 1))
((3, 0), (5, 2))
((3, 1), (0, 1))
((3, 2), (6, 0))
((4, 0), (0, 2))
((4, 1), (7, 1))
((4, 2), (8, 0))
((1, 0), (8, 2))
((1, 1), (9, 1))
((1, 2), (2, 0))
sage: count = 0
sage: for l,p in ts.label_iterator(polygons=True):
....:     print(str(l)+" -> "+str(p))
....:     count=count+1
....:     if count>5:
....:         break
0 -> Polygon(vertices=[(0, 0), (4, 0), (0, 3)])
2 -> Polygon(vertices=[(0, 0), (4, 0), (4, 4), (0, 4)])
3 -> Polygon(vertices=[(0, 0), (-72/25, -21/25), (28/25, -96/25)])
4 -> Polygon(vertices=[(0, 0), (0, 3), (-4, 0)])
1 -> Polygon(vertices=[(0, 0), (0, -3), (4, 0)])
5 -> Polygon(vertices=[(0, 0), (-28/25, 96/25), (-72/25, -21/25)])

change_base_label(new_base_label)

Change the base_label to the provided label.

is_compact()

label_iterator(polygons=False)

Iterator over all polygon labels.

num_polygons()

Return the number of polygons making up the surface in constant time.

opposite_edge(p, e=None)

Given the label p of a polygon and an edge e in that polygon returns the pair (pp, ee) to which this edge is glued.

polygon(lab)

Return the polygon with label lab.

flatsurf.geometry.surface_legacy.TranslationSurface(surface, *args, **kwargs)

Refine the category of surface.

This function is deprecated and should not be used anymore.

EXAMPLES:

sage: from flatsurf import Surface_list, polygons, TranslationSurface
sage: S = Surface_list(QQ)
sage: S.add_polygon(polygons.square())
0
sage: S.set_edge_pairing(0, 0, 0, 2)
sage: S.set_edge_pairing(0, 1, 0, 3)
sage: S = TranslationSurface(S)
doctest:warning
...
UserWarning: TranslationSurface() has been deprecated and will be removed in a future version of sage-flatsurf; there is no distinction between an (underlying) Surface and the SimilaritySurface types anymore.
Calling set_immutable() on this surface should determine the category of this surface automatically so calling TranslationSurface() should not be necessary in this case.
You can still explicitly refine the category of a surface with _refine_category_() but this is not recommended.
We will now refine the category of this surface to make sure that it is in the Category of connected without boundary translation surfaces.
sage: S.category()
Category of connected without boundary finite type translation surfaces
sage: S.set_immutable()
sage: S.category()
Category of connected without boundary finite type translation surfaces

flatsurf.geometry.surface_legacy.surface_list_from_polygons_and_gluings(polygons, gluings, mutable=False)

Take a list of polygons and gluings (given either as a list of pairs of edges, or as a dictionary), and produce a Surface_list from it. The mutable parameter determines the mutability of the resulting surface.